【数学】立体几何

线

若有

• $\vec{n}$：线的方向
• $\vec{p}$：线的位置
• $\vec{a}$：线上任意一点
• $t$：点 $\vec{a}$ 相对线位置的法向偏移关系

则根据线的性质有：$\vec{a} = \vec{n}t +\vec{p}$

即 a 点为：

$\begin{cases} \vec{a}_x=\vec{n}_xt+\vec{p}_x\\ \vec{a}_y=\vec{n}_yt+\vec{p}_y\\ \vec{a}_z=\vec{n}_zt+\vec{p}_z\\ \end{cases}$

由此可得出直线的参数方程：

$$\begin{cases} x=\vec{n}_xt+\vec{p}_x\\ y=\vec{n}_yt+\vec{p}_y\\ z=\vec{n}_zt+\vec{p}_z\\ \end{cases}$$

或对称式方程：

$$\frac{x-\vec{p}_x}{\vec{n}_x}=\frac{y-\vec{p}_y}{\vec{n}_y}=\frac{z-\vec{p}_z}{\vec{n}_z}=t$$

• $\vec{n}$：线的方向
• $\vec{p}$：线的位置
• $t$：线上任意点的位置系数

面

若有

• $\vec{n}$：平面的法线
• $\vec{p}$：平面的位置
• $\vec{a}$：平面上任意一点

则根据平面的性质有：

$\begin{aligned} \vec{n} \cdot (\vec{a}-\vec{p}) &=0 \\ \vec{n} \cdot \vec{a} - \vec{n} \cdot \vec{p} &= 0\\ \vec{n}_x\vec{a}_x + \vec{n}_y\vec{a}_y +\vec{n}_z\vec{a}_z -\vec{n} \cdot \vec{p} &= 0\\ \end{aligned}$

由此可得出平面的一般式方程：

$$Ax+By+Cz+D=0$$

• $A=\vec{n}_x$
• $B=\vec{n}_y$
• $C=\vec{n}_z$
• $D=-(\vec{n} \cdot \vec{p})$

面与线交点

多面体

棱柱

棱锥

非多面体

圆柱

圆锥

球

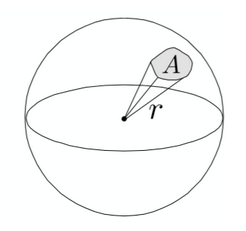
立体角

alt text

角在三维空间中的衍生。

$$\Omega = \frac{A}{r^2}$$

球的总计角度为 $4\pi$。

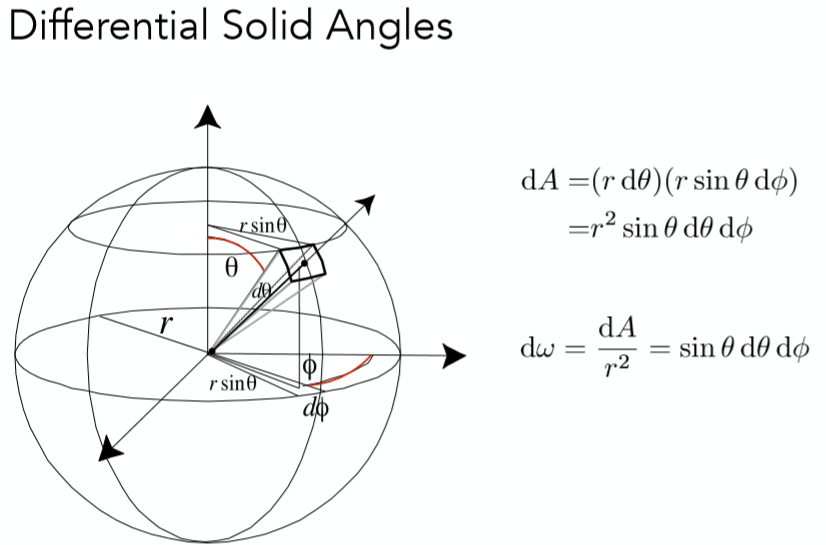
微分立体角

当立体角中的$A$为最小值时得到的立体角。

alt text